Basic Concepts

On this webpage, we show how to test the following null hypothesis:

H₀: the regression line doesn’t capture the relationship between the variables

If we reject the null hypothesis it means that the line is a good fit for the data. We now express the null hypothesis in a way that is more easily testable:

H₀:  ≤ 

As described in Two Sample Hypothesis Testing to Compare Variances, we can use the F test to compare the variances in two samples. To test the above null hypothesis we set F = MS_Reg/MS_Res and use df_Reg, df_Res degrees of freedom.

Assumptions

The use of the linear regression model is based on the following assumptions:

• Linearity of the phenomenon measured
• Constant variance of the error term
• Independence of the error terms
• Normality of the error term distribution

In fact, the normality assumption is equivalent to the condition that the sample comes from a population with a bivariate normal distribution. See Multivariate Normal Distribution for more information about this distribution. The homogeneity of the variance assumption is equivalent to the condition that for any values x₁ and x₂ of x, the variance of y for those x are equal, i.e.

Linear regression can be effective with a sample size as small as 20.

Example

Example 1: Test whether the regression line in Example 1 of Method of Least Squares is a good fit for the data.

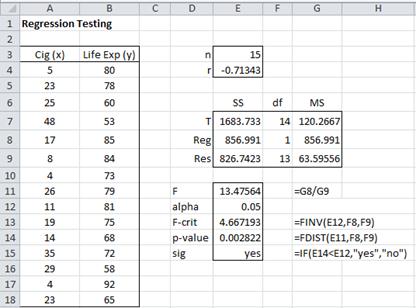
Figure 1 – Goodness of fit of regression line for data in Example 1

We note that SS_T = DEVSQ(B4:B18) = 1683.7 and r = CORREL(A4:A18, B4:B18) = -0.713, and so by Property 3 of Regression Analysis, SS_Reg = r²·SS_T = (1683.7)(0.713)² = 857.0. By Property 1 of Regression Analysis, SS_Res = SS_T – SS_Reg = 1683.7 – 857.0 = 826.7. From these values, it is easy to calculate MS_Reg and MS_Res.

We now calculate the test statistic F = MS_Reg/MS_Res = 857.0/63.6 = 13.5. Since F_crit = F.INV(α, df_Reg, df_Res) = F.INV(.05, 1, 13) = 4.7 < 13.5 = F, we reject the null hypothesis, and so accept that the regression line is a good fit for the data (with 95% confidence). Alternatively, we note that p-value = F.DIST.RT(F, df_Reg, df_Res) = F.DIST.RT(13.5, 1, 13) = 0.0028 < .05 = α, and so once again we reject the null hypothesis.

Observations

There are many ways of calculating SS_Reg, SS_Res, and SS_T. E.g. using the worksheet in Figure 1 of Regression Analysis, we note that SS_Reg = DEVSQ(K5:K19) and SS_Res = DEVSQ(L5:L19). These formulas are valid since the means of the y values and ȳ values are equal by Property 5(b) of Regression Analysis.

Also by Definition 2 of Regression Analysis, SS_Res =  (y_i – ŷ_i)²  = SUMXMY2(J5:J19, K5:K19). Finally, SS_T = DEVSQ(J5:J19), but alternatively SS_T = var(y) ∙ df_T = VAR(J5:J19) * (COUNT(J5:J19)-1).