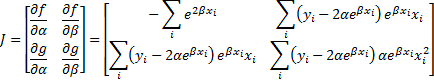Exponential Regression Newton’s Method – Advanced
Property 1: Given samples {x1, …, xn} and {y1, …, yn} and let ŷ = αeβx, then the value of α and β that minimize (yi − ŷi)2 satisfy the following equations:
Proof: The minimum is obtained when the first partial derivatives are 0. Let
Thus we seek values for α and β such that and
; i.e.
Property 2: Under the same assumptions as Property 1, given initial guesses α0 and β0 forα and β, let F = [f g]T where f and g are as in Property 1 and
Now define the 2 × 1 column vectors Bn and the 2 × 2 matrices Jn recursively as follows
Then provided α0 and β0 are sufficiently close to the coefficient values that minimize the sum of the deviations squared, then Bn converges to such coefficient values.
Proof: Now
Thus
The proof now follows by Property 2 of Newton’s Method.